Symmetrische Functies Ontdekken

Stel je voor: een spiegel die de wereld perfect weerspiegelt. Dat is de essentie van een even functie. Maar wat betekent dat precies in de wiskunde? Laten we samen op ontdekkingstocht gaan in de fascinerende wereld van even functies en hun eigenschappen.
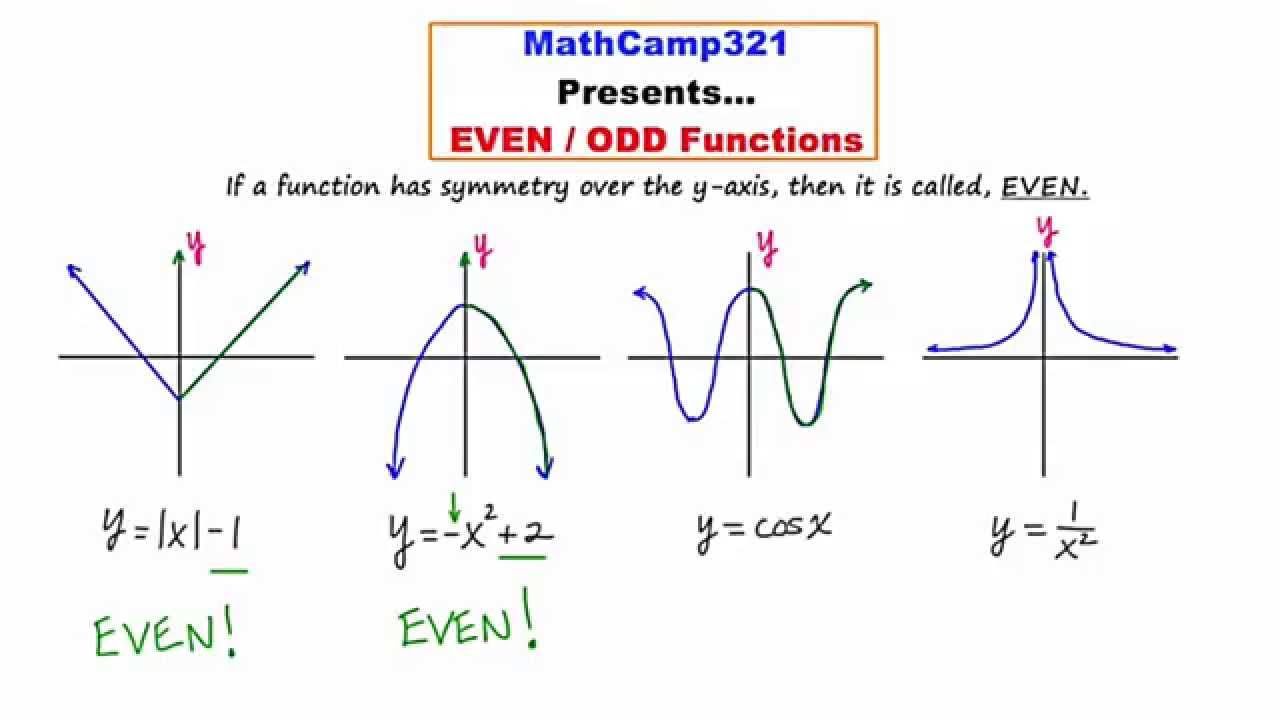
Een even functie is als een kunstwerk dat perfect symmetrisch is ten opzichte van de y-as. Als je de grafiek van een even functie zou vouwen langs de y-as, zouden de twee helften perfect op elkaar vallen. Denk aan de parabool y = x². Aan beide kanten van de y-as zie je dezelfde vorm, een prachtig voorbeeld van een even functie.
Maar waar komen deze functies vandaan en waarom zijn ze belangrijk? Het concept van even en oneven functies vindt zijn oorsprong in de studie van symmetrie, een fundamenteel concept in de wiskunde en natuurkunde. Van de symmetrie in kristallen tot de symmetrie in de wetten van de natuurkunde, even functies spelen een cruciale rol in het modelleren en begrijpen van de wereld om ons heen.
Het herkennen van een even functie kan ons helpen bij het vereenvoudigen van berekeningen en het oplossen van complexe problemen. Door de symmetrie te benutten, kunnen we bijvoorbeeld de integraal van een even functie over een symmetrisch interval vereenvoudigen. Dit is slechts één voorbeeld van de vele praktische toepassingen van even functies in verschillende wetenschappelijke disciplines.
In dit artikel zullen we dieper ingaan op de definitie, voorbeelden en eigenschappen van even functies. We zullen verschillende voorbeelden bekijken, van eenvoudige polynomen tot meer complexe trigonometrische functies. We zullen ook de voordelen en toepassingen van even functies in de wiskunde en natuurkunde bespreken. Bereid je voor om de symmetrie en elegantie van even functies te ontdekken!
Een functie f(x) is even als f(-x) = f(x) voor alle x in het domein van de functie. Dit betekent dat als je x vervangt door -x, de functiewaarde hetzelfde blijft. Neem bijvoorbeeld de functie f(x) = x². Als we x vervangen door -x, krijgen we f(-x) = (-x)² = x², wat gelijk is aan f(x). Dus, f(x) = x² is een even functie. Andere voorbeelden zijn: cos(x), x⁴ + 2x² + 1, en de absolute waarde functie |x|.
Voor- en Nadelen van Even Functies
| Voordelen | Nadelen |
|---|---|
| Vereenvoudiging van berekeningen | Beperkte toepasbaarheid in sommige situaties |
| Symmetrie in grafieken | Niet alle functies zijn even |
Veelgestelde vragen:
1. Wat is een even functie? Antwoord: Een functie waarvoor f(-x) = f(x).
2. Is f(x) = x³ een even functie? Antwoord: Nee, want f(-x) = -x³ ≠ x³.
3. Wat is een voorbeeld van een even trigonometrische functie? Antwoord: cos(x).
4. Hoe test je of een functie even is? Antwoord: Vervang x door -x en kijk of f(-x) = f(x).
5. Zijn alle constante functies even? Antwoord: Ja.
6. Kan een functie zowel even als oneven zijn? Antwoord: Ja, de functie f(x) = 0.
7. Wat is het belang van even functies in de natuurkunde? Antwoord: Ze modelleren symmetrische verschijnselen.
8. Hoe helpt het herkennen van een even functie bij integratie? Antwoord: Het vereenvoudigt de berekening over symmetrische intervallen.
Tips en trucs: Denk aan de grafische representatie om snel te bepalen of een functie even is. Een symmetrische grafiek ten opzichte van de y-as wijst op een even functie.
Conclusie: Even functies zijn een essentieel onderdeel van de wiskunde. Hun symmetrische eigenschappen vereenvoudigen berekeningen en bieden inzichten in diverse wetenschappelijke toepassingen. Van het modelleren van fysische fenomenen tot het oplossen van complexe wiskundige problemen, even functies spelen een onmisbare rol. Door de eigenschappen en voorbeelden in dit artikel te bestuderen, kunnen we een dieper begrip ontwikkelen van deze elegante en krachtige wiskundige concepten. Ga zelf aan de slag met het identificeren en toepassen van even functies en ontdek de symmetrie die schuilgaat in de wiskundige wereld om ons heen. Hopelijk heeft dit artikel je geïnspireerd om verder te duiken in de fascinerende wereld van de wiskunde!
Vijfletterwoorden beginnend met word ontdekken
Ontdek de magie van words of wonders speel en leer
Amy winehouse tattoos costume inspiratie en gids